Longest Increasing Subsequence in C

Last Updated : 11 Jul, 2024

In this article, we will learn how to find the Longest Increasing Subsequence (LIS) of a given sequence using C programming language. LIS is the longest subsequence of a sequence such that all elements of the subsequence are sorted in increasing order.

Example:

Input:
Sequence: [10, 22, 9, 33, 21, 50, 41, 60, 80]

Output:
Length of longest increasing subsequence is: 6

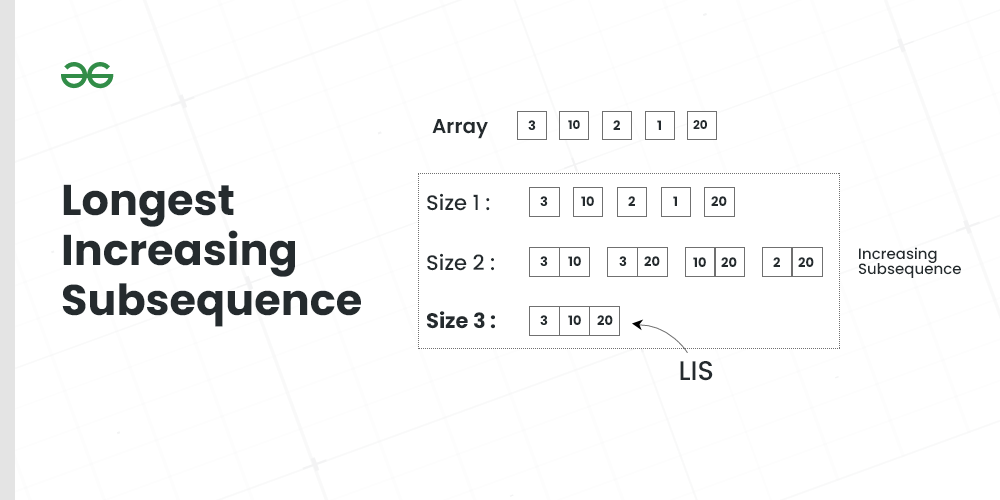
Longest Increasing Subsequence LIS

Table of Content

Method 1: Using Recursion
Method 2: Using Memoization
Method 3: Using Dynamic Programming
Method 4: Using Binary Search

Method 1: Using Recursion

In this approach, we will explore all possible subsequences and select the longest increasing one. By recursively comparing each element with the previous elements, we can determine whether to include it in the subsequence.

Approach

Create a function lisRecursive that takes the array arr, its length n, and an index i.
Base Condition: If the array length is 1, return 1.
Recursively compute the LIS ending at every index.
Compare the current element with the previous element to maintain increasing order and calculate the LIS for each element.
Return the maximum length obtained by including or excluding the current element.

Below is the implementation of the above approach:

// C  program to find longest increasing subsequence using
// recursion

#include <stdio.h>

// Function to return the maximum of two integers
int max(int a, int b) { return (a > b) ? a : b; }

// Recursive function to find the length of the Longest
// Increasing Subsequence (LIS)
int lisRecursive(int arr[], int n, int* max_ref)
{
    // Base case: LIS length of one element is 1
    if (n == 1)
        return 1;
    // Initialize max_ending_here to 1 for the current
    // element
    int res, max_ending_here = 1;

    // Recursively find the LIS ending at each element
    // before arr[n-1]
    for (int i = 1; i < n; i++) {
        res = lisRecursive(arr, i, max_ref);
        // If arr[i-1] is smaller than arr[n-1], and
        // including arr[n-1] results in a longer
        // subsequence
        if (arr[i - 1] < arr[n - 1]
            && res + 1 > max_ending_here)
            max_ending_here = res + 1;
    }

    // Update the maximum LIS length found so far
    if (*max_ref < max_ending_here)
        *max_ref = max_ending_here;
    // Return the LIS length ending at arr[n-1]
    return max_ending_here;
}

// Function to find the length of the Longest Increasing
// Subsequence (LIS) in an array
int lis(int arr[], int n)
{
    // Initialize the maximum LIS length
    int max = 1;
    // Call the recursive function to compute the LIS length
    lisRecursive(arr, n, &max);
    // Return the maximum LIS length found
    return max;
}

int main()
{
    // Input array
    int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60, 80 };
    // Size of the array
    int n = sizeof(arr) / sizeof(arr[0]);
    // Print the length of the Longest Increasing
    // Subsequence (LIS)
    printf("Length of LIS is %d\n", lis(arr, n));
    return 0;
}

Output

Length of LIS is 6

Time Complexity: O(2ⁿ) ,The time complexity of this recursive approach is exponential as there is a case of overlapping subproblems as explained in the recursive tree diagram above.
Auxiliary Space: O(1). No external space is used for storing values apart from the internal stack space.

Method 2: Using Memoization

We can use memoization that optimizes the recursive approach by storing the results of subproblems and reuse them when the same inputs occur again. This prevents redundant calculations and significantly reduces the time complexity.

Approach

Create an array memo to store the LIS for each index.
Implement a function lisMemoization that takes arr, n, and the memoization array memo.
Base Condition: If the array length is 1, return 1.
If the result is already computed, return it.
Recursively compute and store results for the remaining elements.
Return the computed result from the memoization array.

Below is the implementation of the above approach:

// C  program to find longest increasing subsequence using
// Memoization

#include <stdio.h>
#include <string.h>

// Function to return the maximum of two integers
int max(int a, int b) { return (a > b) ? a : b; }

// Function to find the length of the Longest Increasing
// Subsequence (LIS) using memoization
int lisMemoization(int arr[], int n, int* memo)
{
    // If the value is already computed, return it
    if (memo[n] != -1)
        return memo[n];
    // Initialize max_ending_here to 1 for the current
    // element
    int res, max_ending_here = 1;

    // Recursively find the LIS ending at each element
    // before arr[n-1]
    for (int i = 1; i < n; i++) {
        res = lisMemoization(arr, i, memo);
        // If arr[i-1] is smaller than arr[n-1], and
        // including arr[n-1] results in a longer
        // subsequence
        if (arr[i - 1] < arr[n - 1]
            && res + 1 > max_ending_here)
            max_ending_here = res + 1;
    }

    // Store the result in memo array and return it
    return memo[n] = max_ending_here;
}

// Function to find the length of the Longest Increasing
// Subsequence (LIS) in an array
int lis(int arr[], int n)
{
    // Memoization array
    int memo[n + 1];
    // Initialize memo array with -1
    memset(memo, -1, sizeof(memo));
    // Initialize the maximum LIS length
    int maxLength = 1;

    // Compute the LIS length for each element in the array
    for (int i = 1; i <= n; i++)
        maxLength
            = max(maxLength, lisMemoization(arr, i, memo));
    // Return the maximum LIS length found
    return maxLength;
}

int main()
{
    // Input array
    int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60, 80 };
    // Size of the array
    int n = sizeof(arr) / sizeof(arr[0]);
    // Print the length of the Longest Increasing
    // Subsequence (LIS)
    printf("Length of LIS is %d\n", lis(arr, n));
    return 0;
}

Output

Length of LIS is 6

Time Complexity: O(N²)
Auxiliary Space: O(N²)

Method 3: Using Dynamic Programming

In this approach we will iteratively computes the LIS by storing intermediate results, making the process more efficient.

Approach

Create an array lis of size n and initialize all values to 1.
Iterate through the array to fill the table based on the increasing subsequences.
or each element, find the longest subsequence ending at that element.
Return the result i.e. the maximum value in the lis array will be the length of the LIS.

Below is the implementation of the above approach:

// C  program to find longest increasing subsequence using
// dynamic programming

#include <stdio.h>

// Function to return the maximum of two integers
int max(int a, int b) { return (a > b) ? a : b; }

// Function to find the length of the Longest Increasing
// Subsequence (LIS) using tabulation
int lisTabulation(int arr[], int n)
{
    // Array to store the LIS values for each index
    int lis[n];

    // Initialize LIS values for all indexes as 1
    for (int i = 0; i < n; i++)
        lis[i] = 1;

    // Compute optimized LIS values in a bottom-up manner
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < i; j++) {
            // If arr[i] is greater than arr[j] and LIS at i
            // is less than LIS at j plus one, update LIS at
            // i
            if (arr[i] > arr[j] && lis[i] < lis[j] + 1)
                lis[i] = lis[j] + 1;
        }
    }

    // Find the maximum value in the lis array, which is the
    // length of the longest increasing subsequence
    int maxLength = 0;
    for (int i = 0; i < n; i++)
        maxLength = max(maxLength, lis[i]);
    // Return the length of the LIS
    return maxLength;
}

int main()
{
    // Input array
    int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60, 80 };
    // Size of the array
    int n = sizeof(arr) / sizeof(arr[0]);

    // Print the length of the Longest Increasing
    // Subsequence (LIS)
    printf("Length of LIS is %d\n", lisTabulation(arr, n));

    return 0;
}

Output

Length of LIS is 6

Time Complexity: O(N²), as a nested loop is used.
Auxiliary Space: O(N), use of any array to store LIS values at each index.

Method 4: Using Binary Search

We can use the binary search to improve the time complexity by efficiently finding the position where the current element should be placed in the subsequence.

Approach

Create an array tail to store the smallest ending element of all increasing subsequences of length i+1.
Start with the first element of the input array.
For each element, use binary search to find its position in the tail array.
If the element is larger than the largest element in tail, extend tail. Otherwise, replace the existing element in tail.
Return the result i.e. the length of the tail array is the length of the LIS.

Below is the implementation of the above approach:

// C  program to find longest increasing subsequence using
// binary search

#include <stdio.h>

// Function to perform binary search on the 'tail' array
// It returns the index of the smallest number greater than
// or equal to 'key'
int binarySearch(int* tail, int l, int r, int key)
{
    while (r - l > 1) {
        // Calculate mid point
        int m = l + (r - l) / 2;
        // If middle element is greater than or equal to key
        // Search in the left half
        if (tail[m] >= key)
            r = m;
        else
            // Search in the right half
            l = m;
    }
    // Return the index where key should be placed
    return r;
}

// Function to find the length of the Longest Increasing
// Subsequence (LIS) using binary search
int lisBinarySearch(int arr[], int n)
{
    if (n == 0)
        return 0;
    // Array to store the end elements of potential LIS
    int tail[n];
    // Initialize the length of LIS
    int length = 1;
    // First element is the start of the LIS
    tail[0] = arr[0];
    for (int i = 1; i < n; i++) {
        // New smallest element
        if (arr[i] < tail[0])
            tail[0] = arr[i];
        // Extend the existing LIS
        else if (arr[i] > tail[length - 1])
            tail[length++] = arr[i];
        else // arr[i] will replace an element in tail
            tail[binarySearch(tail, -1, length - 1, arr[i])]
                = arr[i];
    }
    // Return the length of the LIS
    return length;
}
int main()
{

    // input array
    int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60, 80 };
    // calculate size of the array
    int n = sizeof(arr) / sizeof(arr[0]);
    // print the LIS
    printf("Length of LIS is %d\n",
           lisBinarySearch(arr, n));
    return 0;
}

Output

Length of LIS is 6

Time Complexity: O(n log n)
Auxiliary Space: O(n), as it uses additional space linearly proportional to the size of the input array arr, primarily for storing the tail array.