Introduction to Bitwise Algorithms – Data Structures and Algorithms Tutorial
Bit stands for binary digit. A bit is the basic unit of information and can only have one of two possible values that is 0 or 1. In our world, we usually with numbers using the decimal base. In other words. we use the digit 0 to 9 However, there are other number representations that can be quite useful such as the binary number systems.

Introduction to Bitwise Algorithms – Data Structures and Algorithms Tutorial
Unlike humans, computers have no concepts of words and numbers. They receive data encoded at the lowest level as a series of zeros and ones (0 and 1). These are called bits, and they are the basis for all the commands they receive. We’ll begin by learning about bits and then explore a few algorithms for manipulating bits. We’ll then explore a few algorithms for manipulating bits. The tutorial is meant to be an introduction to bit algorithms for programmers.
Table of Content
What is Bitwise Algorithms?
Bitwise algorithms refer to algorithms that perform operations on individual bits or bit patterns within computer data. These algorithms uses the binary representation of data and use the fundamental bitwise operations such as AND, OR, XOR, NOT, and bit shifting to manipulate and extract information from the data.
Bitwise algorithms are usually faster and use less memory than regular arithmetic operations because they work directly with the binary representation of data. This often leads to faster execution times and reduced memory usage.
Bitwise Operators / Basics of Bit manipulation
An algorithmic operation known as bit manipulation involves the manipulation of bits at the bit level (bitwise). Bit manipulation is all about these bitwise operations. They improve the efficiency of programs by being primitive, fast actions.
The computer uses this bit manipulation to perform operations like addition, subtraction, multiplication, and division are all done at the bit level. This operation is performed in the arithmetic logic unit (ALU) which is a part of a computer’s CPU. Inside the ALU, all such mathematical operations are performed.
There are different bitwise operations used in bit manipulation. These bit operations operate on the individual bits of the bit patterns. Bit operations are fast and can be used in optimizing time complexity.
The main bitwise operators are:
- AND (&)
- OR (|)
- XOR (^)
- NOT (~)
- Left Shift (<<)
- Right Shift (>>)
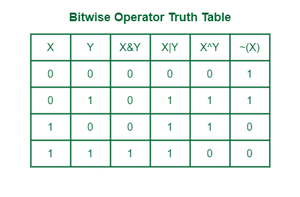
Bitwise Operator Truth Table
Bitwise AND Operator (&)
The bitwise AND operator is denoted using a single ampersand symbol, i.e. &. The & operator takes two equal-length bit patterns as parameters. The two-bit integers are compared. If the bits in the compared positions of the bit patterns are 1, then the resulting bit is 1. If not, it is 0.
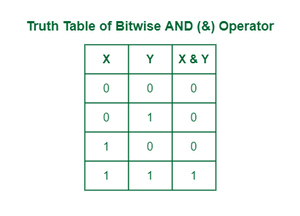
Truth table of AND operator
Example:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise and of both X & y
Bitwise ANDof (7 & 4)
Implementation of AND operator:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 7, b = 4;
int result = a & b;
cout << result << endl;
return 0;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main (String[] args) {
int a = 7, b = 4;
int result = a & b;
System.out.println(result);
}
}
// This code is contributed by lokeshmvs21.
a = 7
b = 4
result = a & b
print(result)
# This code is contributed by akashish__
using System;
public class GFG{
static public void Main (){
int a = 7, b = 4;
int result = a & b;
Console.WriteLine(result);
}
}
// This code is contributed by akashish__
let a = 7, b = 4;
let result = a & b;
console.log(result);
// This code is contributed by akashish__
Output
4
Time Complexity: O(1)
Auxiliary Space: O(1)
Bitwise OR Operator (|)
The | Operator takes two equivalent length bit designs as boundaries; if the two bits in the looked-at position are 0, the next bit is zero. If not, it is 1.
.png)
Example:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise OR of both X, y
Bitwise OR of (7 | 4)
Explanation: On the basis of truth table of bitwise OR operator we can conclude that the result of
1 | 1 = 1
1 | 0 = 1
0 | 1 = 1
0 | 0 = 0We used the similar concept of bitwise operator that are show in the image.
Implementation of OR operator:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 12, b = 25;
int result = a | b;
cout << result;
return 0;
}
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 12, b = 25;
int result = a | b;
System.out.println(result);
}
}
a = 12
b = 25
result = a | b
print(result)
# This code is contributed by garg28harsh.
using System;
public class GFG{
static public void Main (){
int a = 12, b = 25;
int result = a | b;
Console.WriteLine(result);
}
}
// This code is contributed by akashish__
let a = 12, b = 25;
let result = a | b;
document.write(result);
// This code is contributed by garg28harsh.
Output
29
Time Complexity: O(1)
Auxiliary Space: O(1)
Bitwise XOR Operator (^)
The ^ operator (also known as the XOR operator) stands for Exclusive Or. Here, if bits in the compared position do not match their resulting bit is 1. i.e, The result of the bitwise XOR operator is 1 if the corresponding bits of two operands are opposite, otherwise 0.
.png)
Example:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise and of both X & y
Bitwise OR of (7 ^ 4)
Explanation: On the basis of truth table of bitwise XOR operator we can conclude that the result of
1 ^ 1 = 0
1 ^ 0 = 1
0 ^ 1 = 1
0 ^ 0 = 0We used the similar concept of bitwise operator that are show in the image.
Implementation of XOR operator:
#include <iostream>
using namespace std;
int main()
{
int a = 12, b = 25;
cout << (a ^ b);
return 0;
}
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 12, b = 25;
int result = a ^ b;
System.out.println(result);
}
}
// This code is contributed by garg28harsh.
a = 12
b = 25
result = a ^ b
print(result)
# This code is contributed by garg28harsh.
// C# Code
using System;
public class GFG {
static public void Main()
{
// Code
int a = 12, b = 25;
int result = a ^ b;
Console.WriteLine(result);
}
}
// This code is contributed by lokesh
let a = 12;
let b = 25;
console.log((a ^ b));
// This code is contributed by akashish__
Output
21
Time Complexity: O(1)
Auxiliary Space: O(1)
Bitwise NOT Operator (!~)
All the above three bitwise operators are binary operators (i.e, requiring two operands in order to operate). Unlike other bitwise operators, this one requires only one operand to operate.
The bitwise Not Operator takes a single value and returns its one’s complement. The one’s complement of a binary number is obtained by toggling all bits in it, i.e, transforming the 0 bit to 1 and the 1 bit to 0.

Truth Table of Bitwise Operator NOT
Example:
Take two bit values X and Y, where X = 5= (101)2 . Take Bitwise NOT of X.
Explanation: On the basis of truth table of bitwise NOT operator we can conclude that the result of
~1 = 0
~0 = 1We used the similar concept of bitwise operator that are show in the image.
Implementation of NOT operator:
#include <iostream>
using namespace std;
int main()
{
int a = 0;
cout << "Value of a without using NOT operator: " << a;
cout << "\nInverting using NOT operator (with sign bit): " << (~a);
cout << "\nInverting using NOT operator (without sign bit): " << (!a);
return 0;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 0;
System.out.println(
"Value of a without using NOT operator: " + a);
System.out.println(
"Inverting using NOT operator (with sign bit): "
+ (~a));
if (a != 1)
System.out.println(
"Inverting using NOT operator (without sign bit): 1");
else
System.out.println(
"Inverting using NOT operator (without sign bit): 0");
}
}
// This code is contributed by lokesh.
a = 0
print("Value of a without using NOT operator: " , a)
print("Inverting using NOT operator (with sign bit): " , (~a))
print("Inverting using NOT operator (without sign bit): " , int(not(a)))
# This code is contributed by akashish__
using System;
public class GFG {
static public void Main()
{
int a = 0;
Console.WriteLine(
"Value of a without using NOT operator: " + a);
Console.WriteLine(
"Inverting using NOT operator (with sign bit): "
+ (~a));
if (a != 1)
Console.WriteLine(
"Inverting using NOT operator (without sign bit): 1");
else
Console.WriteLine(
"Inverting using NOT operator (without sign bit): 0");
}
}
// This code is contributed by akashish__
let a =0;
document.write("Value of a without using NOT operator: " + a);
document.write( "Inverting using NOT operator (with sign bit): " + (~a));
if(!a)
document.write( "Inverting using NOT operator (without sign bit): 1" );
else
document.write( "Inverting using NOT operator (without sign bit): 0" );
Output
Value of a without using NOT operator: 0 Inverting using NOT operator (with sign bit): -1 Inverting using NOT operator (without sign bit): 1
Time Complexity: O(1)
Auxiliary Space: O(1)
Left-Shift (<<)
The left shift operator is denoted by the double left arrow key (<<). The general syntax for left shift is shift-expression << k. The left-shift operator causes the bits in shift expression to be shifted to the left by the number of positions specified by k. The bit positions that the shift operation has vacated are zero-filled.
Note: Every time we shift a number towards the left by 1 bit it multiply that number by 2.

Logical left Shift
Example:
Input: Left shift of 5 by 1.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 1)
Left shift of 5 by 1
Output: 10
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010102, Which is equivalent to 10Input: Left shift of 5 by 2.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 2)Left shift of 5 by 2
Output: 20
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 101002, Which is equivalent to 20Input: Left shift of 5 by 3.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 3)Left shift of 5 by 3
Output: 40
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010002, Which is equivalent to 40
Implementation of Left shift operator:
#include <bits/stdc++.h>
using namespace std;
int main()
{
unsigned int num1 = 1024;
bitset<32> bt1(num1);
cout << bt1 << endl;
unsigned int num2 = num1 << 1;
bitset<32> bt2(num2);
cout << bt2 << endl;
unsigned int num3 = num1 << 2;
bitset<16> bitset13{ num3 };
cout << bitset13 << endl;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num1 = 1024;
String bt1 = Integer.toBinaryString(num1);
bt1 = String.format("%32s", bt1).replace(' ', '0');
System.out.println(bt1);
int num2 = num1 << 1;
String bt2 = Integer.toBinaryString(num2);
bt2 = String.format("%32s", bt2).replace(' ', '0');
System.out.println(bt2);
int num3 = num1 << 2;
String bitset13 = Integer.toBinaryString(num3);
bitset13 = String.format("%16s", bitset13)
.replace(' ', '0');
System.out.println(bitset13);
}
}
// This code is contributed by akashish__
# Python code for the above approach
num1 = 1024
bt1 = bin(num1)[2:].zfill(32)
print(bt1)
num2 = num1 << 1
bt2 = bin(num2)[2:].zfill(32)
print(bt2)
num3 = num1 << 2
bitset13 = bin(num3)[2:].zfill(16)
print(bitset13)
# This code is contributed by Prince Kumar
using System;
class GFG {
public static void Main(string[] args)
{
int num1 = 1024;
string bt1 = Convert.ToString(num1, 2);
bt1 = bt1.PadLeft(32, '0');
Console.WriteLine(bt1);
int num2 = num1 << 1;
string bt2 = Convert.ToString(num2, 2);
bt2 = bt2.PadLeft(32, '0');
Console.WriteLine(bt2);
int num3 = num1 << 2;
string bitset13 = Convert.ToString(num3, 2);
bitset13 = bitset13.PadLeft(16, '0');
Console.WriteLine(bitset13);
}
}
// This code is contributed by akashish__
// JavaScript code for the above approach
let num1 = 1024;
let bt1 = num1.toString(2).padStart(32, '0');
console.log(bt1);
let num2 = num1 << 1;
let bt2 = num2.toString(2).padStart(32, '0');
console.log(bt2);
let num3 = num1 << 2;
let bitset13 = num3.toString(2).padStart(16, '0');
console.log(bitset13);
Output
00000000000000000000010000000000 00000000000000000000100000000000 0001000000000000
Time Complexity: O(1)
Auxiliary Space: O(1)
Right-Shift (>>)
The right shift operator is denoted by the double right arrow key (>>). The general syntax for the right shift is “shift-expression >> k”. The right-shift operator causes the bits in shift expression to be shifted to the right by the number of positions specified by k. For unsigned numbers, the bit positions that the shift operation has vacated are zero-filled. For signed numbers, the sign bit is used to fill the vacated bit positions. In other words, if the number is positive, 0 is used, and if the number is negative, 1 is used.
Note: Every time we shift a number towards the right by 1 bit it divides that number by 2.
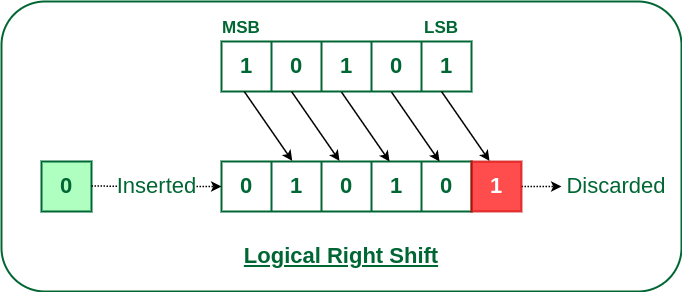
Logical Right Shift
Example:
Input: Right shift of 5 by 1.
Binary representation of 5 = 00101 and Right shift of 00101 by 1 (i.e, 00101 >> 1)Right shift of 5 by 1
Output: 2
Explanation: All bit of 5 will be shifted by 1 to Rightside and this result in 00010 Which is equivalent to 2Input: Right shift of 5 by 2.
Binary representation of 5 = 00101 and Right shift of 00101 by 2 (i.e, 00101 >> 2)Right shift of 5 by 2
Output: 1
Explanation: All bit of 5 will be shifted by 2 to Right side and this result in 00001, Which is equivalent to 1Input: Right shift of 5 by 3.
Binary representation of 5 = 00101 and Right shift of 00101 by 3 (i.e, 00101 >> 3)Right shift of 5 by 3
Output: 0
Explanation: All bit of 5 will be shifted by 3 to Right side and this result in 00000, Which is equivalent to 0
Implementation of Right shift operator:
#include <bitset>
#include <iostream>
using namespace std;
int main()
{
unsigned int num1 = 1024;
bitset<32> bt1(num1);
cout << bt1 << endl;
unsigned int num2 = num1 >> 1;
bitset<32> bt2(num2);
cout << bt2 << endl;
unsigned int num3 = num1 >> 2;
bitset<16> bitset13{ num3 };
cout << bitset13 << endl;
}
// JavaScript code for the above approach
let num1 = 1024;
let bt1 = num1.toString(2).padStart(32, '0');
console.log(bt1);
let num2 = num1 >> 1;
let bt2 = num2.toString(2).padStart(32, '0');
console.log(bt2);
let num3 = num1 >> 2;
let bitset13 = num3.toString(2).padStart(16, '0');
console.log(bitset13);
// akashish__
Output
00000000000000000000010000000000 00000000000000000000001000000000 0000000100000000
Time Complexity: O(1)
Auxiliary Space: O(1)
Application of Bit Operators
- Bit operations are used for the optimization of embedded systems.
- The Exclusive-or operator can be used to confirm the integrity of a file, making sure it has not been corrupted, especially after it has been in transit.
- Bitwise operations are used in Data encryption and compression.
- Bits are used in the area of networking, framing the packets of numerous bits which are sent to another system generally through any type of serial interface.
- Digital Image Processors use bitwise operations to enhance image pixels and to extract different sections of a microscopic image.
Important Practice Problems on Bitwise Algorithm:
1. How to Set a bit in the number?
If we want to set a bit at nth position in the number ‘num’, it can be done using the ‘OR’ operator( | ).
- First, we left shift 1 to n position via (1<<n)
- Then, use the “OR” operator to set the bit at that position. “OR” operator is used because it will set the bit even if the bit is unset previously in the binary representation of the number ‘num’.
Note: If the bit would be already set then it would remain unchanged.
Below is the implementation:
#include <iostream>
using namespace std;
// num is the number and pos is the position
// at which we want to set the bit.
void set(int& num, int pos)
{
// First step is shift '1', second
// step is bitwise OR
num |= (1 << pos);
}
int main()
{
int num = 4, pos = 1;
set(num, pos);
cout << (int)(num) << endl;
return 0;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 4, pos = 1;
num = set(num, pos);
System.out.println(num);
}
public static int set(int num, int pos)
{
// First step is shift '1', second
// step is bitwise OR
num |= (1 << pos);
return num;
}
}
// This code is contributed by geeky01adash.
# num = number, pos = position at which we want to set the bit
def set(num, pos):
# First step = Shift '1'
# Second step = Bitwise OR
num |= (1 << pos)
print(num)
num, pos = 4, 1
set(num, pos)
# This code is contributed by sarajadhav12052009
using System;
public class GFG {
static public void Main()
{
int num = 4, pos = 1;
set(num, pos);
}
// num = number, pos = position at which we want to set
// the bit
static public void set(int num, int pos)
{
// First Step: Shift '1'
// Second Step: Bitwise OR
num |= (1 << pos);
Console.WriteLine(num);
}
}
// This code is contributed by sarajadhav12052009
<script>
// num is the number and pos is the position
// at which we want to set the bit.
function set(num,pos)
{
// First step is shift '1', second
// step is bitwise OR
num |= (1 << pos);
console.log(parseInt(num));
}
let num = 4;
let pos = 1;
set(num, pos);
// This code is contributed by akashish__
</script>
Output
6
Time Complexity: O(1)
Auxiliary Space: O(1)
2. How to unset/clear a bit at n’th position in the number
Suppose we want to unset a bit at nth position in number ‘num’ then we have to do this with the help of “AND” (&) operator.
- First, we left shift ‘1’ to n position via (1<<n) then we use bitwise NOT operator ‘~’ to unset this shifted ‘1’.
- Now after clearing this left shifted ‘1’ i.e making it to ‘0’ we will ‘AND'(&) with the number ‘num’ that will unset bit at nth position.
Below is the implementation:
#include <iostream>
using namespace std;
// First step is to get a number that has all 1's except
// the given position.
void unset(int& num, int pos)
{
// Second step is to bitwise and this number with given
// number
num &= (~(1 << pos));
}
int main()
{
int num = 7;
int pos = 1;
unset(num, pos);
cout << num << endl;
return 0;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 7, pos = 1;
num = unset(num, pos);
System.out.println(num);
}
public static int unset(int num, int pos)
{
// Second step is to bitwise and this number with
// given number
num = num & (~(1 << pos));
return num;
}
}
# First Step: Getting which have all '1's except the
# given position
def unset(num, pos):
# Second Step: Bitwise AND this number with the given number
num &= (~(1 << pos))
print(num)
num, pos = 7, 1
unset(num, pos)
using System;
public class GFG {
static public void Main()
{
// First Step: Getting a number which have all '1's
// except the given position
int num = 7, pos = 1;
unset(num, pos);
}
static public void unset(int num, int pos)
{
// Second Step: Bitwise AND this number with the
// given number
num &= (~(1 << pos));
Console.WriteLine(num);
}
}
// First step is to get a number that has all 1's except
// the given position.
function unset(num, pos)
{
// Second step is to bitwise and this number with given
// number
return num &= (~(1 << pos));
}
let num = 7;
let pos = 1;
console.log(unset(num, pos));
// contributed by akashish__
Output
5
Time Complexity: O(1)
Auxiliary Space: O(1)
3. Toggling a bit at nth position
Toggling means to turn bit ‘on'(1) if it was ‘off'(0) and to turn ‘off'(0) if it was ‘on'(1) previously. We will be using the ‘XOR’ operator here which is this ‘^’. The reason behind the ‘XOR’ operator is because of its properties.
- Properties of ‘XOR’ operator.
- 1^1 = 0
- 0^0 = 0
- 1^0 = 1
- 0^1 = 1
- If two bits are different then the ‘XOR’ operator returns a set bit(1) else it returns an unset bit(0).
Below is the implementation:
#include <iostream>
using namespace std;
// First step is to shift 1,Second step is to XOR with given
// number
void toggle(int& num, int pos) { num ^= (1 << pos); }
int main()
{
int num = 4;
int pos = 1;
toggle(num, pos);
cout << num << endl;
return 0;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 4, pos = 1;
num = toggle(num, pos);
System.out.println(num);
}
public static int toggle(int num, int pos)
{
// First step is to shift 1,Second step is to XOR
// with given number
num ^= (1 << pos);
return num;
}
}
// This code is contributed by geeky01adash.
def toggle(num, pos):
# First Step: Shifts '1'
# Second Step: XOR num
num ^= (1 << pos)
print(num)
num, pos = 4, 1
toggle(num, pos)
# This code is contributed by sarajadhav12052009
using System;
public class GFG {
static public void Main()
{
int num = 4, pos = 1;
toggle(num, pos);
}
static public void toggle(int num, int pos)
{
// First Step: Shift '1'
// Second Step: XOR num
num ^= (1 << pos);
Console.WriteLine(num);
}
}
// This code is contributed by sarajadhav12052009
// First step is to shift 1,Second step is to XOR with given
// number
function toggle(num, pos){
// First Step: Shifts '1'
// Second Step: XOR num
num ^= (1 << pos)
console.log(num)
}
let num = 4;
let pos = 1;
toggle(num, pos);
// contributed by akashish__
Output
6
Time Complexity: O(1)
Auxiliary Space: O(1)
4. Checking if the bit at nth position is Set or Unset
We used the left shift (<<) operation on 1 to shift the bits to nth position and then use the & operation with number given number, and check if it is not-equals to 0.
Below is the implementation:
#include <iostream>
using namespace std;
bool at_position(int num, int pos)
{
bool bit = num & (1 << pos);
return bit;
}
int main()
{
int num = 5;
int pos = 2;
bool bit = at_position(num, pos);
cout << bit << endl;
return 0;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 5;
int pos = 0;
int bit = at_position(num, pos);
System.out.println(bit);
}
public static int at_position(int num, int pos)
{
int bit = num & (1 << pos);
return bit;
}
}
# code
def at_position(num, pos):
bit = num & (1 << pos)
return bit
num = 5
pos = 0
bit = at_position(num, pos)
print(bit)
using System;
public class GFG {
public static bool at_position(int num, int pos)
{
int bit = num & (1 << pos);
if (bit == 0)
return false;
return true;
}
static public void Main()
{
int num = 5;
int pos = 2;
bool bit = at_position(num, pos);
Console.WriteLine(bit);
}
}
// This code is contributed by akashish__
<script>
function at_position(num,pos)
{
return num & (1<<pos);
}
let num = 5;
let pos = 0;
console.log(at_position(num, pos));
// contributed by akashish__
</script>
Output
1
Time Complexity: O(1)
Auxiliary Space: O(1)
5. Multiply a number by 2 using the left shift operator
Below is the implementation:
#include <iostream>
using namespace std;
int main()
{
int num = 12;
int ans = num << 1;
cout << ans << endl;
return 0;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 12;
int ans = num << 1;
System.out.println(ans);
}
}
// This code is contributed by geeky01adash.
# Python program for the above approach
num = 12
ans = num << 1
print(ans)
# This code is contributed by Shubham Singh
using System;
public class GFG {
static public void Main()
{
int num = 12;
Console.WriteLine(num << 1);
}
}
// This code is contributed by sarajadhav12052009
<script>
// Javascript program for the above approach
var num = 12;
var ans = num<<1;
document.write(ans);
//This code is contributed by Shubham Singh
</script>
Output
24
Time Complexity: O(1)
Auxiliary Space: O(1)
6. Divide a number 2 using the right shift operator
Below is the implementation:
#include <iostream>
using namespace std;
int main()
{
int num = 12;
int ans = num >> 1;
cout << ans << endl;
return 0;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 12;
int ans = num >> 1;
System.out.println(ans);
}
}
// This code is contributed by geeky01adash.
# Python program for the above approach
num = 12
ans = num >> 1
print(ans)
# This code is contributed by Shubham Singh
using System;
public class GFG {
static public void Main()
{
int num = 12;
Console.WriteLine(num >> 1);
}
}
// This code is contributed by sarajadhav12052009
<script>
// Javascript program for the above approach
var num = 12;
var ans = num>>1;
document.write(ans);
//This code is contributed by Shubham Singh
</script>
Output
6
Time Complexity: O(1)
Auxiliary Space: O(1)
7. Compute XOR from 1 to n (direct method)
The problem can be solved based on the following observations:
Say x = n % 4. The XOR value depends on the value if x.
If, x = 0, then the answer is n.
x = 1, then answer is 1.
x = 2, then answer is n+1.
x = 3, then answer is 0.
Below is the implementation of the above approach.
// Direct XOR of all numbers from 1 to n
int computeXOR(int n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
// Direct XOR of all numbers from 1 to n
public static int computeXOR(int n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
public static void main(String[] args) {}
}
// This code is contributed by akashish__
# num = number, pos = position at which we want to set the bit
def set(num, pos):
# First step = Shift '1'
# Second step = Bitwise OR
num |= (1 << pos)
print(num)
num, pos = 4, 1
set(num, pos)
# This code is contributed by sarajadhav12052009
using System;
public class GFG {
// Direct XOR of all numbers from 1 to n
public static int computeXOR(int n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
public static void Main() {}
}
// This code is contributed by akashish__
<script>
// Direct XOR of all numbers from 1 to n
function computeXOR(n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
// This code is contributed by Shubham Singh
</script>
Time Complexity: O(1)
Auxiliary Space: O(1)
8. How to know if a number is a power of 2?
This can be solved based on the following fact:
If a number N is a power of 2, then the bitwise AND of N and N-1 will be 0. But this will not work if N is 0. So just check these two conditions, if any of these two conditions is true.
Below is the implementation of the above approach.
// Function to check if x is power of 2
bool isPowerOfTwo(int x)
{
// First x in the below expression is
// for the case when x is 0
return x && (!(x & (x - 1)));
}
// Function to check if x is power of 2
public static boolean isPowerOfTwo(int x)
{
// First x in the below expression is
// for the case when x is 0
return x != 0 && ((x & (x - 1)) == 0);
}
# Function to check if x is power of 2
def isPowerOfTwo(x):
# First x in the below expression is
# for the case when x is 0
return x and (not(x & (x - 1)))
# This code is contributed by akashish__
using System;
public class GFG {
// Function to check if x is power of 2
static public bool isPowerOfTwo(int x)
{
// First x in the below expression is
// for the case when x is 0
return (x != 0) && ((x & (x - 1)) == 0);
}
static public void Main() {}
}
// This code is contributed by akashish__
// Function to check if x is power of 2
function isPowerOfTwo(x)
{
// First x in the below expression is
// for the case when x is 0
return x && (!(x & (x - 1)));
}
// contributed by akashish__
Time Complexity: O(1)
Auxiliary Space: O(1)
9. Count Set bits in an integer
Counting set bits means, counting total number of 1’s in the binary representation of an integer. For this problem we go through all the bits of given number and check whether it is set or not by performing AND operation (with 1).
Below is the implementation:
// Function to calculate the number of set bits.
int countBits(int n)
{
// Initialising a variable count to 0.
int count = 0;
while (n) {
// If the last bit is 1, count will be incremented
// by 1 in this step.
count += n & 1;
// Using the right shift operator.
// The bits will be shifted one position to the
// right.
n >>= 1;
}
return count;
}
// Function to calculate the number of set bits.
public static int countBits(int n)
{
// Initialising a variable count to 0.
int count = 0;
while (n > 0) {
// If the last bit is 1, count will be incremented
// by 1 in this step.
count += n & 1;
// Using the right shift operator.
// The bits will be shifted one position to the
// right.
n >>= 1;
}
return count;
}
def countBits(n):
# Initializing a variable count to 0
count = 0
while n:
# If the last bit is 1, count will be incremented by 1 in this step.
count += n & 1
# Using the right shift operator. The bits will be shifted one position to the right.
n >>= 1
return count
using System;
public class GFG {
// Function to calculate the number of set bits.
public static int countBits(int n)
{
// Initialising a variable count to 0.
int count = 0;
while (n > 0)
{
// If the last bit is 1, count will be
// incremented by 1 in this step.
count += n & 1;
// Using the right shift operator.
// The bits will be shifted one position to the
// right.
n >>= 1;
}
return count;
}
static public void Main() {}
}
// This code is contributed by akashish__
// Function to calculate the number of set bits.
function countBits(n)
{
// Initialising a variable count to 0.
let count = 0;
while (n) {
// If the last bit is 1, count will be incremented
// by 1 in this step.
count += n & 1;
// Using the right shift operator.
// The bits will be shifted one position to the
// right.
n >>= 1;
}
return count;
}
Time Complexity: O(log(n))
Auxiliary Space: O(1)
10. Position of rightmost set bit
The idea is to unset the rightmost bit of number n and XOR the result with n. Then the rightmost set bit in n will be the position of the only set bit in the result. Note that if n is odd, we can directly return 1 as the first bit is always set for odd numbers.
Example:
The number 20 in binary is 00010100, and the position of the rightmost set bit is 3.
00010100 & (n = 20)
00010011 (n-1 = 19)
——————-
00010000 ^ (XOR result number with n)
00010100
——————-
00000100 ——-> rightmost set bit will tell us the position
Below is the implementation:
// Returns the position of the rightmost set bit of `n`
int positionOfRightmostSetBit(int n)
{
// if the number is odd, return 1
if (n & 1) {
return 1;
}
// unset rightmost bit and xor with the number itself
n = n ^ (n & (n - 1));
// find the position of the only set bit in the result;
// we can directly return `log2(n) + 1` from the
// function
int pos = 0;
while (n) {
n = n >> 1;
pos++;
}
return pos;
}
// Returns the position of the rightmost set bit of `n`
public static int positionOfRightmostSetBit(int n)
{
// if the number is odd, return 1
if ((n & 1) != 0) {
return 1;
}
// unset rightmost bit and xor with the number itself
n = n ^ (n & (n - 1));
// find the position of the only set bit in the result;
// we can directly return `log2(n) + 1` from the
// function
int pos = 0;
while (n != 0) {
n = n >> 1;
pos++;
}
return pos;
}
# Returns the position of the rightmost set bit of `n`
def positionOfRightmostSetBit(n):
# if the number is odd, return 1
if n & 1:
return 1
# unset rightmost bit and xor with the number itself
n = n ^ (n & (n - 1))
# find the position of the only set bit in the result;
# we can directly return `log2(n) + 1` from the function
pos = 0
while n:
n = n >> 1
pos = pos + 1
return pos
// Returns the position of the rightmost set bit of `n`
public static int positionOfRightmostSetBit(int n)
{
// if the number is odd, return 1
if ((n & 1) != 0) {
return 1;
}
// unset rightmost bit and xor with the number itself
n = n ^ (n & (n - 1));
// find the position of the only set bit in the result;
// we can directly return `log2(n) + 1` from the
// function
int pos = 0;
while (n != 0) {
n = n >> 1;
pos++;
}
return pos;
}
// Returns the position of the rightmost set bit of `n`
function positionOfRightmostSetBit( n)
{
// if the number is odd, return 1
if (n & 1) {
return 1;
}
// unset rightmost bit and xor with the number itself
n = n ^ (n & (n - 1));
// find the position of the only set bit in the result;
// we can directly return `log2(n) + 1` from the
// function
let pos = 0;
while (n) {
n = n >> 1;
pos++;
}
return pos;
}
Time Complexity: O(log(n))
Auxiliary Space: O(1)
Frequently Asked Questions (FAQs) on Bitwise Algorithms:
1. What are Bitwise Algorithms?
Bitwise algorithms refer to algorithms that perform operations on individual bits or bit patterns within computer data. These algorithms uses the binary representation of data and use the fundamental bitwise operations such as AND, OR, XOR, NOT, and bit shifting to manipulate and extract information from the data.
2. What are the different types of Bitwise Algorithms?
There are many different types of bitwise algorithms, each with its own purpose. Some common types include:
- AND: Checks if two bits are both on.
- OR: Checks if either or both bits are on.
- XOR: Checks if only one of the bits is on.
- NOT: Flips the state of a bit (on becomes off, off becomes on).
- Shifting: Moves bits left or right to change their value.
3. What are some real-world examples of Bitwise Algorithms?
Bitwise algorithms are used in many different applications, including:
- Image compression: Combining multiple pixels into a single value to save space.
- Cryptography: Encrypting and decrypting data by manipulating bits.
- Error detection and correction: Identifying and fixing errors in data transmission.
- Low-level programming: Optimizing code for speed and efficiency.
4. Why are Bitwise Algorithms important?
Bitwise algorithms are important because they allow us to manipulate data at the most fundamental level. This gives us fine-grained control over how data is stored and processed, which can lead to significant performance improvements.
5. Where can I learn more about Bitwise Algorithms?
There are many resources available online to learn more about bitwise algorithms. Including GeeksforGeeks, Wikipedia
Related article:
- Bits manipulation (Important tactics)
- Bitwise Hacks for Competitive Programming
- Bit Tricks for Competitive Programming
- More Practice Problems on Bitwise Algorithms











.png)